MATRICES ESPECIALES
Matriz identidad:
esta es una matriz cuadrada , donde el numero de filas es igual al numero de columnas, y esta formada por unos (1) en forma diagonal y ceros(0) en las demas posiciones.
sus potencias son ellas mismas, su matriz inversa es ella misma,solo tiene un valor propio que es 1. es una matriz permutación.
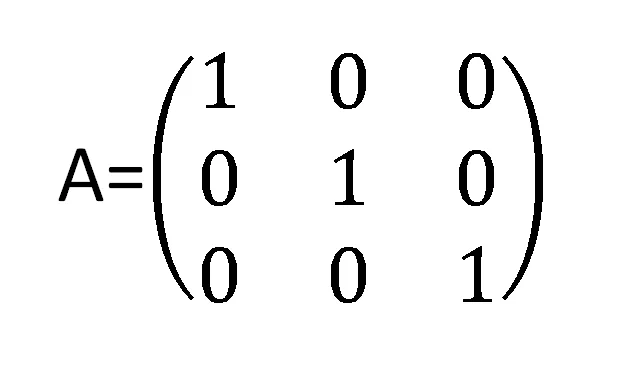
Matriz diagonal:
es una matriz diagonal por que los elementos que no estan diagonalmente equivalen a ceros., por lo tanto una matriz identidad tambien es una matriz diagonal.
en las matrices cuadradas el determinante son los numeros que estan en la diagonal. y son regulares si, y solo si los elementos de la diaonal son diferentes de ceros.
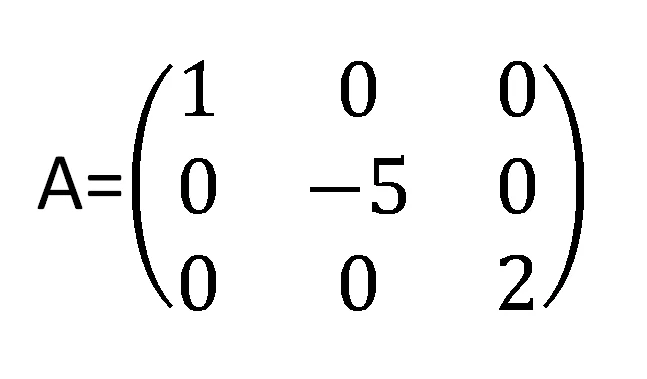
Matriz triangular superior:
Es una matriz superior solo si tiene ceros por debajo de la diagonal.
![]()
Matriz triangular inferior:
Es una matriz triangularinferior solo si tiene los ceros por encima de la diagonal 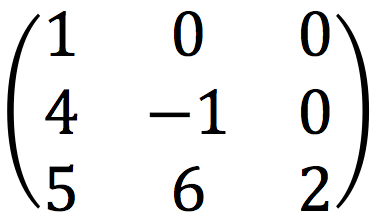
la inversa de una matriz triangular superior-(infeior) es una matriz superior-(inferior).
sus valores propios son los elementos de la diagonal.
Matriz simétrica:
Una matriz es simétrica solo si es igual a su traspuesta, es decir, la matriz tiene que ser cuadrada.
La inversa de una matriz simétrica regular es simétrica.
La adjunta de una simétrica es simétrica,La suma de simétricas es simétrica. El producto lo es si, y sólo si, también es conmutativo. los valores propios de una matriz cuadrada, real y simétrica son reales.los vectores propios de autovalores distintos de una matriz cuadrada y real son ortogonales.

La matriz traspuesta de una matriz A se denota por A^T y se obtiene cambiando sus filas por columnas (o viceversa).
Ejemplo:
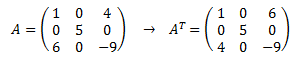
No hay comentarios:
Publicar un comentario